Diese Seite funktioniert nur mit Javascript.
Große Nutzenmöglichkeitskurve5.2.3 Soziale WohlfahrtsfunktionenDas Optimum Optimorum
ine Wohlfahrtsfunktion ist eine "Nutzenfunktion für die Gesellschaft". Vielleicht wissen Sie schon, dass eine "gesellschaftliche Präferenzordnung", in der die individuellen Präferenzen konsistent aufgehen, selbst bei gewissen minimalen Anforderungen nicht existiert - oder etwas präziser formuliert, dass sich bereits bei recht schwach erscheinenden Anforderungen kein Mechanismus finden lässt, der die individuellen zu einer gesellschaftlichen Präferenzordnung konsistent zusammenführt (sog. Unmöglichkeitstheorem). Wenngleich später noch einmal die Rede davon sein wird, ignorieren wir dieses Problem zunächst, indem wir im folgenden von der Annahme einer kardinalen Messbarkeit der individuellen Nutzen ausgehen, ohne dass wir uns hier weiter damit aufhalten wollen.
Bevor wir die Eigenschaften einer aus einer Wohlfahrtsfunktion abgeleiteten sozialen Indifferenzkurve untersuchen, soll zunächst der Wohlfahrtsbegriff erörtert werden; der Begriff Wohlfahrtsfunktion wurde übrigens in der Form "economic welfare function" von Bergson geprägt, weswegen auch mitunter von Bergson-Indifferenzkurven die Rede ist.
Beinahe jedes Lehrbuch der Wirtschaftspolitik dürfte eine Definition des Wohlfahrtsbegriffes enthalten. Sie alle weichen mehr oder weniger voneinander ab. Eine recht allgemeine, zudem recht ansprechende, stammt von Giersch, da wir hier kaum eine kaum eine bessere entwickeln können, geben wir sie wieder:
Es lassen sich verschiedene Arten solcher Funktionen unterscheiden. So kann man z.B. von einer ökonomischen Wohlfahrtsfunktion sprechen, wenn man alle Variablen nicht-ökonomischer Natur (ich kenne übrigens keine - Sie vielleicht?) ausschließt. Andere Arten von Wohlfahrtsfunktionen werden durch die sie klassifizierenden Adjektive soweit erklärt, dass hier auf eine weitere Erörterung verzichtet werden kann, z.B. ordinale, kardinale, diktatorische, kurzfristige, langfristige, nationale Wohlfahrtsfunktionen. Wichtige Unterscheidungen sollen jedoch kurz erklärt werden:
- 1.) Individuelle/Soziale Wohlfahrtsfunktion
Diese Unterscheidung wird getroffen, je nachdem ob die Wohlfahrt eines einzelnen oder einer Gruppe untersucht werden soll. Die individuelle Wohlfahrtsfunktion ist die bekannte Nutzenfunktion - also ein Spezialfall -, die, die hier interessiert, die Soziale Wohlfahrtsfunktion, in die die Nutzen von Konsument und Konsumentin eingehen.
- 2.) Persönliche Soziale Wohlfahrtsfunktion
In dieser Bezeichnung soll zum Ausdruck kommen, dass ein bestimmtes Individuum die Soziale Wohlfahrtsfunktion nach eigenen Vorstellungen aufgestellt hat. Die persönliche Soziale Wohlfahrtsfunktion eines anderen könnte ganz andere Gestalt haben.
- 3.) Individualistische Soziale Wohlfahrtsfunktion
Diese Bezeichnung wird in der Literatur in zwei verschiedenen Varianten benutzt. Zum einen soll sie andeuten, dass alle Mitglieder einer sozialen Gruppe einer Situationsänderung zuzustimmen hätten, wenn sie positiv bewertet werden soll, zum anderen, dass sich das Wohlfahrtsniveau einzig und allein mit den Nutzenniveaus von Individuen, nicht jedoch durch andere Faktoren ändern soll.
- Arrows Auffassung einer Sozialen Wohlfahrtsfunktion
Arrow fasst eine Soziale Wohlfahrtsfunktion als Aggregationsregel für die individuellen Präferenzordnungen auf. Wir kommen gleich darauf zurück.
- 5.) Paretianische Soziale Wohlfahrtsfunktion
Für eine paretianische Soziale Wohlfahrtsfunktion gilt, dass die Erhörung des Nutzens eines Mitglieds der Gesellschaft positiven Einfluss auf die gesellschaftliche Wohlfahrt ausübt. Eine Veränderung, die durch eine paretianische Wohlfahrtsfunktion positiv bewertet wird, muss nicht notwendigerweise das Pareto-Kriterium erfüllen. Andererseits bedeutet eine Erfüllung des Kriteriums jedoch immer eine positive Veränderung im Sinne einer paretianischen Wohlfahrtsfunktion.
- 6.) Rawls Auffassung einer Sozialen Wohlfahrtsfunktion
Nach Rawls Theorie der Gerechtigkeit sind Wohlfahrtsfunktionen derart zu gestalten, dass Veränderungen, die zu sozialen und wirtschaftlichen Ungleichheiten führen, solange positiv zu werten sind, solange sie jedermanns Vorteil dienen und niemand diskriminiert oder in seinen Grundrechten eingeschränkt wird. Die Regel lässt sich dahingehend interpretieren, dass der Nutzen des am schlechtesten gestellten Individuums zu maximieren ist.
- 7.) Egalitäre Soziale Wohlfahrtsfunktion
In dieser Version werden Situationen, die sich gegenüber anderen durch eine "gleichere" Verteilung der Nutzen auszeichnen, je nach Anwendung des Egalitätsprinzips strikt oder tendenziell vorgezogen.
Im weiteren betrachten wir eine persönlich, individualistische Soziale Wohlfahrtsfunktion paretianischen Typs eines rationalen Individuums i
\[{W_i} = {W_i}\left( {{U_M},{U_W}} \right)\tag{1}\]Mithilfe des Pareto-Kriteriums lassen sich einige Eigenschaften der aus der Wohlfahrtsfunktion (1) ableitbaren Bergson-Indifferenzkurven angeben.
Betrachten wir als Ausgangssituation den Punkt P0 im Nutzenraum in Abbildung 1.
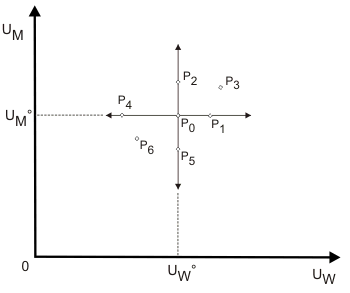
P0 verkörpert für den Konsumenten und die Konsumentin bestimmte Nutzenniveaus $U_M^0$ und $U_W^0$. Durch Einsetzen dieser beiden Werte in die Wohlfahrtsfunktion (1) erhalten wir ein gesellschaftliches Wohlfahrtsniveau, das als $W_0$ gekennzeichnet sei. Eine Bergson-Indifferenzkurve hat die Eigenschaft, dass alle Punkte auf ihr eben dieses Wohlfahrtsniveau $W_0$ anzeigen. Da das Wohlfahrtsniveau mit den individuellen Nutzen von Konsument und Konsumentin steigt, können die Punkte $P_1$, $P_2$ und $P_3$ nicht auf dieser Bergson-Indifferenzkurve liegen, sondern würden jeweils ein höheres Nutzenniveau anzeigen als $P_0$. Dabei kann a priori nicht ausgeschlossen werden, dass $P_1$ und $P_2$ auf derselben Bergson-Indifferenzkurve liegen. Ebenso können wir schließen, dass $P_4$, $P_5$ und $P_6$ nicht Punkte der Bergson-Indifferenzkurve durch $P_0$ sein können. Damit bleibt für den Verlauf der Kurve nur der (streng) nordwestliche und südöstliche Bereich von $P_1$.
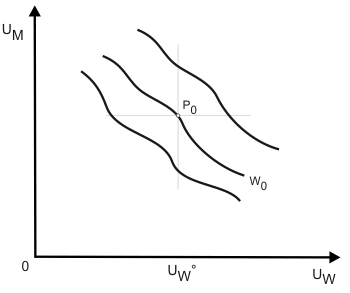
Zwar können sich Bergson-Indifferenzkurven einer konsistenten Wohlfahrtsfunktion nicht schneiden, doch sind weitere Aussagen über ihre Gestalt wegen der ordinalen Nutzenskalen nicht möglich. Abbildung 2 zeigt eine Schar von Bergson-Indifferenzkurven einer konsistenten Wohlfahrtsfunktion.